Выпускной Экзамен Школ МЦАДО по Математике 10.06.2002 г.
Билет N 2
 |
| Билет N 1 |
 |
| Билет N 2 |
 |
| Билет N 3 |
 |
| Билет N 4 |
 |
| Билет N 5 |
 |
| Билет N 6 |
 |
| Билет N 7 |
 |
| Билет N 8 |
 |
| Билет N 9 |
 |
| Билет N 10 |
 |
| Ответы |
 |
| Для Печати |
 |
|
Найдите сумму всех целочисленных решений неравенства  . .
| ||
|
На промежутке | ||
| Из пунктов A и B навстречу друг другу отправились пешеход и велосипедист. Их встреча состоялась через t минут. После встречи пешеход продолжал свой путь в B, велосипедист же повернул назад и тоже поехал в B. Пешеход пришел в B на u минут позже велосипедиста. Найдите t, зная, что скорость пешехода в k раз меньше скорости велосипедиста: u = 45, k = 4. | ||
|
Вычислите | ||
|
Внутри правильного шестиугольника, длина стороны которого равна a, находится окружность радиуса r, касающаяся двух соседних сторон шестиугольника и проходящая через его центр. Найдите a, зная, что r = 12 / (3 + | ||
|
Найдите решения (в градусах) уравнения. В ответ запишите те из них, которые принадлежат отрезку  . .
| ||
|
Найдите все значения a, при которых решения системы неравенств образуют на числовой оси отрезок длины, равной 1: | ||
|
Два шара радиуса r и шар радиуса R касаются каждый двух оставшихся и плоскости | ||
| Точка P лежит на стороне AB, а точка Q на стороне BC треугольника ABC, причем AP : PB = 1 : p; BQ : QC = 1 : q. Через вершину B и точку пересечения отрезков AQ и CP проведена прямая, пересекающая сторону AC в точке R. Во сколько раз отрезок AC длинее отрезка AR ? p = 9, q = 4. | ||
|
Найдите наименьшее расстояние d между точками, одна из которых принадлежит графику функции | ||
 найдите наименьшее и наибольшее решения уравнения
(ответ запишите в градусах):
найдите наименьшее и наибольшее решения уравнения
(ответ запишите в градусах):  .
.
 .
.
 ).
).
 :
: ,
,  .
.
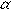 . Шар радиуса
. Шар радиуса  < r касается трех данных и плоскости
< r касается трех данных и плоскости  , а другая графику функции y = A
, а другая графику функции y = A (в ответ запишите квадрат найденного значения d):
(в ответ запишите квадрат найденного значения d):  =
=  ; A = 4.
; A = 4.