Олимпиада по Математике 03.03.2002 г.
Билет N 5
 |
| Билет N 1 |
 |
| Билет N 2 |
 |
| Билет N 3 |
 |
| Билет N 4 |
 |
| Билет N 5 |
 |
| Билет N 6 |
 |
| Билет N 7 |
 |
| Билет N 8 |
 |
| Билет N 9 |
 |
| Билет N 10 |
 |
| Ответы |
 |
| Для Печати |
 |
| Найти сумму всех четырехзначных натуральных чисел, которые при деление на k дают остаток, равный r ; k = 899, r = 422. | |||||
|
Найти все целочисленные решения (x, y) сисетмы неравенств (в ответ записать значения x): | |||||
|
Найти все значения x, удоволтеворяющие уравнению. В ответ записать значения x (в градусах), принадлежащие отрезку 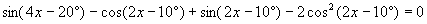 . .
| |||||
| Некоторые из 15 больших коробок содержат по 7 средних коробок. Некоторые из средних коробок содержат по 7 маленьких. Среди всех коробок 99 пустых. Сколько всего коробок? | |||||
|
Решить уравнение: | |||||
|
Вычислить | |||||
|
Решить уравнение: | |||||
|
Найти все значение параметра a, для которых наименьшее значение функции | |||||
| Около шара, описан усеченный конус, площадь нижнего основания которого в 6,25 раз больше площади его верхнего основания. Во сколько раз объем усеченного конуса больше объема шара? | |||||
| Дана трапеция ABCD, причем BC = a, AD = b. Параллельно основаниям BC и AD трапеции проведена прямая, пересекающая сторону AB в точке P, диагональ AC в точке L, диагональ BD в точке R и сторону CD в точке Q. Известно, что PL = LR. Найти длину отрезка PQ ; a = 4, b = 7. | | | |
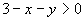 ,
, 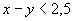 ,
, 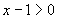 .
.
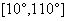 :
: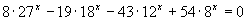
 , если x удовлетворяет уравнению
, если x удовлетворяет уравнению 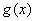 = 0:
= 0:  ,
,  .
.

 меньше c (в ответ записать наименьшее и наибольшее целые значения параметра a, удовлтеворяющее этому условию):
меньше c (в ответ записать наименьшее и наибольшее целые значения параметра a, удовлтеворяющее этому условию):  =
=  , c = 1,25.
, c = 1,25.