Вступительные Экзамены по Математике (1-ый Поток) 16.07.2002 г.
Билет N 2
 |
| Билет N 1 |
 |
| Билет N 2 |
 |
| Билет N 3 |
 |
| Билет N 4 |
 |
| Билет N 5 |
 |
| Билет N 6 |
 |
| Билет N 7 |
 |
| Билет N 8 |
 |
| Билет N 9 |
 |
| Билет N 10 |
 |
| Ответы |
 |
| Для Печати |
 |
|
Решить уравнение | |||||
|
Решить неравенство (в ответ записать сумму целых значений x, удовлетворяющих этому неравенству): | |||||
| Два велосипедиста выезжают одновременно из пункта A с различными скоростями и едут к пункту B. Достигнув его, они тотчас же едут обратно. Первый велосипедист, ехавший быстрее второго, на обратном пути встречает второго на расстоянии a км от B; затем достигнув A, едет снова по направлению к B и, пройдя k-ю часть пути AB, встречает второго велосипедиста, возвращающегося из B. Чему равно расстояние от A до B (в км)? a = 2, k = 3. | |||||
| Последовательность чисел 1, 11, 31, 61, ... обладает тем свойством, что разности двух соседних членов (последующего и предыдущего) образуют арифметическую прогрессию 10, 20, 30, ... . Найти номер члена последовательности, равного 59951. | |||||
|
Вычислить | |||||
|
Вычислить | |||||
| Длины оснований трапеции равны a и b. Чему равна длина отрезка, соединяющего середины диагоналей трапеции? a = 12, b = 7. | |||||
| Найти все значения a, при которых данное неравенство справедливо для всех x (в ответ записть наименьшее значение a, удовлетворяющее этому условию): 
| |||||
|
Найти все целочисленные значения n, при которых значение выражения | |||||
| В треугольнике ABC, площадь которого равна S, проведены биссектриса CE и медиана BD, пересекающиеся в точке O. Чему равна площадь четырехугольника ADOE, если BC = a, AC = b? S = 9, a = 8, b = 4. | | | |
 .
.
 .
.
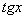 , если
, если 
 , если x, y, z удовлетворяют системе уравнений
, если x, y, z удовлетворяют системе уравнений 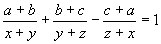 ,
, 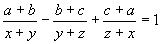 ,
,  ;
;  , a = 2, b = 1, c = 4.
, a = 2, b = 1, c = 4.
 является целым числом. В ответ записать наименьшее n, удовлетворяющее этому условию.
является целым числом. В ответ записать наименьшее n, удовлетворяющее этому условию.