|
|
| | |
| | |
Решить уравнение: 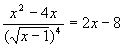 . .
| | | | | | |
Решить уравнение: 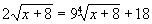 . .
| | | | | | |
Решив неравенство 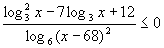 , найдите середины полученных промежутков. , найдите середины полученных промежутков.
| | | | | | |
Найти x из системы: 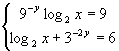 . .
| | | | | | |
Найти коэффициент p квадратного уравнения 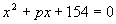 , если известно, что его корни положительны и их разность равна 3. , если известно, что его корни положительны и их разность равна 3.
| | | | | | |
Биссектрисы тупых углов при основании трапеции, длина которого равна 21, пересекаются в точке, лежащей на противоположном основании. Длины этих биссектрис равны 22,5 и 19,5. Найти площадь трапеции.
| | | | | | |
Найдите x в градусах, если 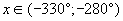 и и 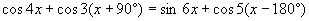 . .
| | | | | | |
Найти объем правильной шестиугольной призмы, если известно, что радиус шара, касающегося всех ребер этой призмы равен 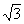 . .
| | | | | | |
Найти наименьшее и наибольшее целое значение параметра a, при котором неравенство 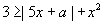 имеет хотя бы одно неотрицательное решение. имеет хотя бы одно неотрицательное решение.
| | | | | | |
Шины, установленные на передних колесах автомобиля, полностью изнашиваются и подлежат замене после 30 000 км пробега. Те же шины, установленные на задних колесах, выдерживают 50 000 км. Какое максимальное расстояние сможет проехать автомобиль на одном комплекте шин, если шины на передних и задних колесах своевременно поменять местами?
| |
| | | |
|
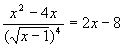 .
.
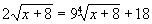 .
.
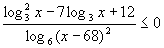 , найдите середины полученных промежутков.
, найдите середины полученных промежутков.
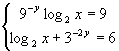 .
.
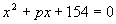 , если известно, что его корни положительны и их разность равна 3.
, если известно, что его корни положительны и их разность равна 3.
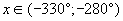 и
и 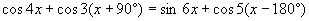 .
.
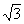 .
.
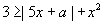 имеет хотя бы одно неотрицательное решение.
имеет хотя бы одно неотрицательное решение.