|
|
| | |
| | |
Решить уравнение:  . .
| | | | | | |
Решить уравнение: 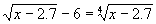 . .
| | | | | | |
Решив неравенство 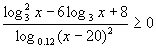 , найдите середины полученных промежутков. , найдите середины полученных промежутков.
| | | | | | |
Найти x из системы: 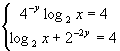 . .
| | | | | | |
Найти коэффициент p квадратного уравнения 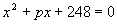 , если известно, что его корни положительны и их разность равна 23. , если известно, что его корни положительны и их разность равна 23.
| | | | | | |
Биссектрисы тупых углов при основании трапеции, длина которого равна 21, пересекаются в точке, лежащей на средней линии трапеции. Длины этих биссектрис равны 45 и 39. Найти длины боковых сторон трапеции.
| | | | | | |
Найдите x в градусах, если 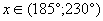 и и 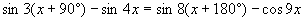 . .
| | | | | | |
Найти радиус шара, касающегося всех ребер правильной восьмиугольной призмы, если известно, что высота этой призмы равна 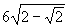 . .
| | | | | | |
Найти наименьшее и наибольшее целое значение параметра a, при котором неравенство 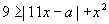 имеет хотя бы одно неотрицательное решение. имеет хотя бы одно неотрицательное решение.
| | | | | | |
На автомобиле стоят два одинаковых номерных знака, которые можно менять местами - один спереди, другой сзади. Знак, стоящий сзади, за 9 лет эксплуатации приходит в негодность и подлежит замене. Знак, стоящий спереди, приходит в негодность вдвое быстрее. Износ можно считать пропорциональным времени. Какой максимальный срок (в годах) сможет прослужить один комплект из двух номерных знаков, если своевременно поменять передний и задний номерной знак местами?
| |
| | | |
|
 .
.
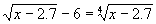 .
.
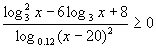 , найдите середины полученных промежутков.
, найдите середины полученных промежутков.
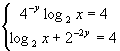 .
.
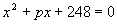 , если известно, что его корни положительны и их разность равна 23.
, если известно, что его корни положительны и их разность равна 23.
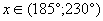 и
и 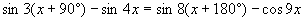 .
.
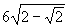 .
.
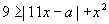 имеет хотя бы одно неотрицательное решение.
имеет хотя бы одно неотрицательное решение.