| | |
|
| |
Решить уравнение: 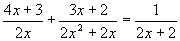 . .
|
| | | |
| |
Найти середины промежутков конечной длины, на которых выполнено неравенство: 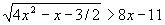 . .
|
| | | |
| |
Решить уравнение: 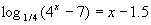 . .
|
| | | |
| |
Найти y из системы: 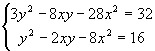 . .
|
| | | |
| |
Найдите x в градусах, если 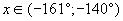 и и 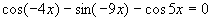 . .
|
| | | |
| |
Произведение членов геометрической прогрессии с номерами от 13 до 147 равно 5-405. Найти восьмидесятый член прогрессии.
|
| | | |
| |
Бильярдный стол имеет форму правильного треугольника ABC со стороной 3. Шарик ударился последовательно о борт AB в его середине, о борт ВС в точке P и о борт AС на расстоянии 2 от точки A. Найдите расстояние BP.
|
| | | |
| |
В основании пирамиды SABCD с высотой 7 лежит квадрат, площадь которого равна 23. Все плоские углы при вершине А прямые. Точка Е лежит на середине ребра SB, а точка F делит ребро SD в отношении SF : FD = 2 : 1. Через точки A, Е, F проведена плоскость, пересекающая ребро SC в точке G. Найти расстояние от точки G до вершины A.
|
| | | |
| |
Найти графически число корней уравнения 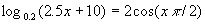 . .
|
| | | |
| |
На новом станке рабочие делают за час целое число деталей, большее, чем 11. На старом станке за то же время делают на 3 детали меньше. Заказ из определенного числа деталей на новом станке выполняют за целое число часов. На двух старых станках заказ такой же величины можно выполнить на 3 часа быстрее. Из какого количества деталей состойт заказ?
|
|
| | | |
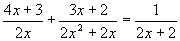 .
.
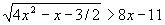 .
.
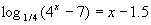 .
.
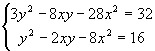 .
.
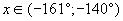 и
и 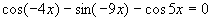 .
.
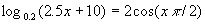 .
.