|
|
| | |
| | |
Упростить и вычислить при a = 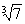 ; b = ; b = 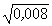 : : 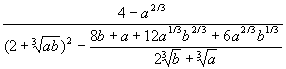 . .
| | | | | | |
Решить уравнение: 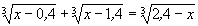 . .
| | | | | | |
Сколько существует целочисленных арифметических прогрессий с ненулевой разностью, первый член которых равен 2, а произведение второго и четвертого членов не превосходит 39?
| | | | | | |
Найти y из системы: 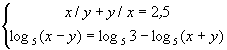 . .
| | | | | | |
Найти сумму и произведение корней уравнения 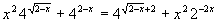 . .
| | | | | | |
В треугольнике  ABC через внутреннюю точку параллельно сторонам проведены три прямые, разбивающие треугольник на 6 частей, три из которых параллелограммы, а три - треугольники с площадями 27, 75, 108. Найти сумму площадей трех параллелограммов. ABC через внутреннюю точку параллельно сторонам проведены три прямые, разбивающие треугольник на 6 частей, три из которых параллелограммы, а три - треугольники с площадями 27, 75, 108. Найти сумму площадей трех параллелограммов.
| | | | | | |
Найдите x в градусах, если 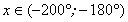 и и 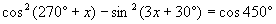 . .
| | | | | | |
В правильную треугольную пирамиду вписан шар радиуса 27. Другой шар, имеющий радиус 9, касается вписанного шара и трех боковых граней пирамиды. Чему равно расстояние от вершины пирамиды до центра шара?
| | | | | | |
Даны три числа. Если утроенный квадрат первого числа сложить с удвоенным квадратом второго числа, а затем с квадратом третьего числа, то получиться 13.5. Если первое число умножить на девять, затем отнять от него удвоенное второе и прибавить третье, умноженное на пять, то получиться 27. Найти сумму этих чисел и квадрат второго числа.
| | | | | | |
Найдите наибольшее значение x, удовлетворяющее неравенству 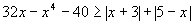 . .
| |
| | | |
|
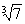 ; b =
; b = 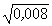 :
: 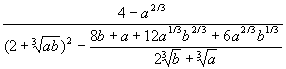 .
.
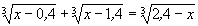 .
.
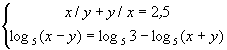 .
.
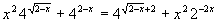 .
.
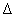 ABC через внутреннюю точку параллельно сторонам проведены три прямые, разбивающие треугольник на 6 частей, три из которых параллелограммы, а три - треугольники с площадями 27, 75, 108. Найти сумму площадей трех параллелограммов.
ABC через внутреннюю точку параллельно сторонам проведены три прямые, разбивающие треугольник на 6 частей, три из которых параллелограммы, а три - треугольники с площадями 27, 75, 108. Найти сумму площадей трех параллелограммов.
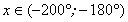 и
и 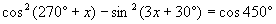 .
.
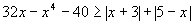 .
.