| | |
|
| |
Упростить и вычислить при x = 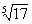 , a = 3: , a = 3: 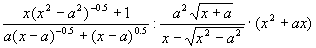 . .
|
| | | |
| |
Решить уравнение: 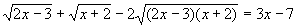 . .
|
| | | |
| |
Сумма десяти первых членов возрастающей геометрической прогрессии в 244 раза больше суммы пяти ее первых членов и в 6 раз больше суммы квадратов тех же пяти членов. Найти четвертый член прогрессии.
|
| | | |
| |
Найти x из системы: 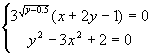 . .
|
| | | |
| |
Найти сумму всех целых значений параметра p, при которых неравенство 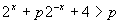 выполняется при всех значениях x. выполняется при всех значениях x.
|
| | | |
| |
Длина образующей конуса равна 25.5, длина окружности основания конуса равана 141.3. Найти периметр осевого сечения и тангенс угла между высотой и образующей конуса. Число 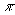 считать равным 3.14. считать равным 3.14.
|
| | | |
| |
Найдите x в градусах, если 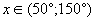 и и  . .
|
| | | |
| |
В треугольнике 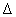 ABC точка D делит сторону BC в отношении BD : DC = 2 : 1, точка E делит сторону AB в отношении AE : EB = 2 : 1, точка F делит сторону AC в отношении AF : FC = 1 : 2. K - точка пересечения отрезков ED и BF. Найти координаты точки K, если координаты вершин A(3; -7), B(-3; 17), C(18; 32). ABC точка D делит сторону BC в отношении BD : DC = 2 : 1, точка E делит сторону AB в отношении AE : EB = 2 : 1, точка F делит сторону AC в отношении AF : FC = 1 : 2. K - точка пересечения отрезков ED и BF. Найти координаты точки K, если координаты вершин A(3; -7), B(-3; 17), C(18; 32).
|
| | | |
| |
Некоторое количество крупы засыпали в мешки вместимостью 32 кг. Один мешок оказался заполнен частично, а остальные полностью. Если бы это же количество крупы засыпали в мешки емкостью 17 кг, то то мешков потребовалось на 21 больше и опять один мешок оказался заполнен частично, а остальные - полностью. Сколько потребовалось бы мешков вместимостью 25 кг, если известно, что все они были бы этим количеством крупы заполнены полностью?
|
| | | |
| |
Найти наименьшее значение x, удовлетворяющее неравенству 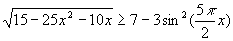 . .
|
|
| | | |
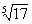 , a = 3:
, a = 3: 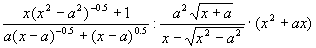 .
.
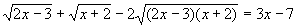 .
.
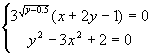 .
.
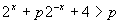 выполняется при всех значениях x.
выполняется при всех значениях x.
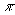 считать равным 3.14.
считать равным 3.14.
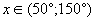 и
и  .
.
 ABC точка D делит сторону BC в отношении BD : DC = 2 : 1, точка E делит сторону AB в отношении AE : EB = 2 : 1, точка F делит сторону AC в отношении AF : FC = 1 : 2. K - точка пересечения отрезков ED и BF. Найти координаты точки K, если координаты вершин A(3; -7), B(-3; 17), C(18; 32).
ABC точка D делит сторону BC в отношении BD : DC = 2 : 1, точка E делит сторону AB в отношении AE : EB = 2 : 1, точка F делит сторону AC в отношении AF : FC = 1 : 2. K - точка пересечения отрезков ED и BF. Найти координаты точки K, если координаты вершин A(3; -7), B(-3; 17), C(18; 32).
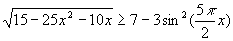 .
.