| | |
|
| |
Решить уравнение:  .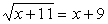
|
| | | |
| |
Пусть f (x) = log12 (12 x + 4). Решить уравнение f (x) = f (0.1 x + 13.5).
|
| | | |
| |
При каком значении m сумма квадратов корней уравненияx2 + (100 – m) x – (m + 11) = 0 наименьшая?
|
| | | |
| |
При каких значениях a нижеприведенная система уравнений имеет ровно два решения  .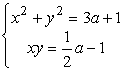
|
| | | |
| |
Решить уравнение: 2 sin2 3 x + 4 cos x cos 2 x cos 3 x = 1. В ответе указать число различных корней, расположенных на промежутке [0°; 180°].
|
| | | |
| |
Найти сумму целых значений параметра a, при которых нижепреведенное уравнение не имеет решений:  .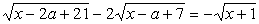
|
| | | |
| |
Два экскаватора вырыли котлован за 24 дня. Первый экскаватор мог бы выполнить эту работу в 1.5 раза быстрее, чем второй. За сколько дней мог бы выполнить эту работу каждый экскаватор по отдельности?
|
| | | |
| |
Найти знаменатель геометрической прогрессии, у которой сумма первого и четвертого членов равна -49, а сумма второго и третьего равна 14.
|
| | | |
| |
Вычислить площадь области (x, y), задаваемой системой неравенств  .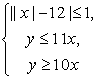
|
| | | |
| |
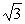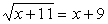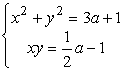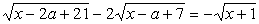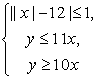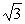В кубе ABCDA'B'C'D' со стороной 2 +  расположены два шара. Один шар вписан в куб. Другой шар, меньшего радиуса, касается внешним образом большого шара и касается трех граней куба, сходящихся к варшине A. Найти радиус меньшего шара.
|
|
| | | |