| | |
|
| |
Решить уравнение:  .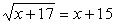
|
| | | |
| |
Пусть f (x) = log5 (5 x + 1). Решить уравнение f (x) = f (0.2 x + 4).
|
| | | |
| |
При каком значении m сумма квадратов корней уравненияx2 + (34 – m) x – (m + 5) = 0 наименьшая?
|
| | | |
| |
При каких значениях a нижеприведенная система уравнений имеет ровно два решения  .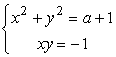
|
| | | |
| |
Решить уравнение: sin2 2 x + 8 sin2 x = 0. В ответе указать число различных корней, расположенных на промежутке [0°; 180°].
|
| | | |
| |
Найти сумму целых значений параметра a, при которых нижепреведенное уравнение не имеет решений:  .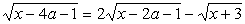
|
| | | |
| |
Две трубы, работая одновременно, наполняют бассейн за 12 часов. Первая труба наполняет бассейн на 10 часов быстрее, чем вторая. За сколько часов наводняет бассейн каждая труба отдельно?
|
| | | |
| |
Найти знаменатель геометрической прогрессии, у которой разность между третьим и первым членами равна 9, разность между пятым и третьим членами, равна 36.
|
| | | |
| |
Вычислить площадь области (x, y), задаваемой системой неравенств  .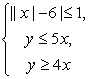
|
| | | |
| |
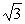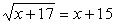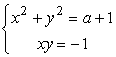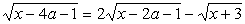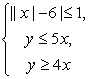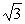В кубе ABCDA'B'C'D' со стороной 4 (3 +  ) расположены два шара, касающиеся внешним образом друг друга. Их радиусы относятся как 1 : 2. Один шар касается трех граней куба, прилежащих к вершине А. Другой шар касается трех граней куба, прилежащих к вершине С' (АС' - диагональ куба). Найти радиусы шаров.
|
|
| | | |