| | |
|
| |
Решить уравнение:  .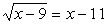
|
| | | |
| |
Пусть f (x) = log4 (6 x – 1). Решить уравнение f (x) = f (0.25 x + 4.5).
|
| | | |
| |
При каком значении m сумма квадратов корней уравненияx2 + (23 – m) x – (m + 4) = 0 наименьшая?
|
| | | |
| |
При каких значениях a нижеприведенная система уравнений имеет ровно два решения  .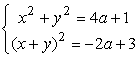
|
| | | |
| |
Решить уравнение: 1 + sin 2 x = cos x + sin x. В ответе указать число различных корней, расположенных на промежутке [0°; 90°].
|
| | | |
| |
Найти сумму целых значений параметра a, при которых нижепреведенное уравнение не имеет решений:  .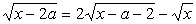
|
| | | |
| |
Чан наполняется двумя кранами. Наполнение чана только первым краном длится на 22 минуты дольше, чем только вторым. Если же открыть оба крана, то чан наполнится за 60 минут. За сколько минут каждый кран отдельно может наполнить чан?
|
| | | |
| |
Найти знаменатель геометрической прогрессии, если сумма первых трех членов прогрессий равна 7, а их произведение равно 8.
|
| | | |
| |
Вычислить площадь области (x, y), задаваемой системой неравенств  .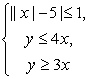
|
| | | |
| |
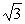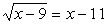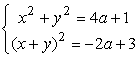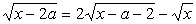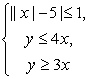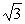В кубе ABCDA'B'C'D' со стороной 3 +  расположены два шара, касающиеся внешним образом друг друга. Их радиусы относятся как 1 : 4. Один шар касается трех граней куба, прилежащих к вершине А. Другой шар касается трех граней куба, прилежащих к вершине С' (АС' - диагональ куба). Найти радиусы шаров.
|
|
| | | |